TD : la file

La file est une structure de données qui permet de stocker des éléments de même nature (on dit encore que la file est un conteneur).

Le premier élément qui est entré dans la file est aussi le premier élément qui en sort. On dit que la polititque de stockage de la file est de type FIFO (First In First Out) ou encore premier entré-premier sorti. Ce modèle correspond tout à fait à la file d'attente que l'on rencontre tous les jours dans la vie courante.

Description fonctionnelle

Voici la description fonctionnelle d'une file sous forme de TAD.

TAD FILE[G]	Types
		`FILE[G]` (G prédéfini)
	Fonctions
		`créer` : FILE[G] `est_vide` : FILE[G] -> booléen `ajouter` : FILE[G] x G -> FILE[G] `enlever` : FILE[G] -> FILE[G] `premier` : FILE[G] -> G
	Axiomes
		A1 : `est_vide(créer) = VRAI` A2 : `est_vide(ajouter(f,x)) = FAUX`A3 : `premier(ajouter(créer,x))=x` A4 : `premier(ajouter(f,x))=premier(f)`A5 : `enlever(ajouter(créer,x))="créer"`A6 : `enlever(ajouter(f,x))= ajouter(enlever(f),x)`	pour tout f, x
	Préconditions
		`enlever` requiert est_vide=FAUX `premier` requiert est_vide= FAUX

L'opération ajouter (ou encore enfiler) a pour rôle d'ajouter un élément en queue de file et l'opération enlever (ou défiler) supprime l'élément en tête de file. Premier retourne le premier élément de la file (i.e. le premier à sortir) et est_vide indique si la file est vide ou pas.

Remarque 1 : La pile et la file disposent des mêmes fonctions mais les axiomes sont fondamentalement différents.

Remarque 2 : Là encore, cette spécification est indépendante de tout langage de programmation.

Description logique

Il existe de nombreuses possibilités (algorithmiques) pour réaliser une file. En particulier, nous devons choisir une représentation en mémoire de la file. Je vous propose ici deux solutions qui utilisent un tableau. Dans les deux cas, nous introduisons le concept de taille d'une file : la taille maximale de la file sera prédéfinie et ne pourra bien évidemment pas excéder la taille du tableau (appelée N).

Dès lors, la file a une taille limite, nous pouvons donc modifier la description fonctionnelle en ajoutant une nouvelle fonction : est_pleine : FILE[G] -> booléen.

Tableau simple

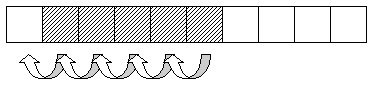
C'est la solution la plus simple mais aussi la plus "lente". La tête de le file se trouve toujours à l'indice 1 du tableau. Le dernier élément entré est connu par son index d. On a toujours : d <= N où N représente la taille maximale de la pile.

A chaque fois qu'un élément est dépilé, il faut décaler tous les autres pour que le premier élément sortant soit à nouveau à l'indice 1.

Travail à faire : On veut réaliser la modélisation objet de la file. Donner les algorithmes des méthodes créer, ajouter et enlever. (Je ne vous empêche pas de faire les autres...)

Tableau "circulaire"

La solution précédente n'est pas satisfaisante car le décalage des éléments prend du temps alors comment s'en passer ? On utilise ce que l'on appelle un tableau "circulaire". On note p l'indice du premier élément de la file et d l'indice du dernier élément.

De quelle manière gère-t'on les indices ?

Si on doit incrémenter un indice se trouvant à la position N, on le place à la position 1 si cela est possible.
Si on doit dérémenter un indice se trouvant à la position 1 on le place à la position N si cela est possible.

Travail à faire : On veut réaliser la modélisation objet de la file. Donner les algorithmes de TOUTES les méthodes de la classe File. Vous pouvez reprendre le modèle de la pile.

Que valent les indices lorsque la file est vide et en particulier à sa création ?
Que valent les indices lorque la file ne contient qu'un élément ?
Bien repérer les différentes configurations des indices.
Expliciter les cas d'erreurs lors des opérations d'ajout et de suppression.

Description physique

La partie difficile a été faite dans la description logique.

(1) Écrire uniquement la déclaration de la classe TFile en Delphi, et non pas l'implémentation des méthodes.
(2) En travail personnel, vous pourrez écrire un programme similaire à celui écrit pour le TP sur la pile.